College Algebra I – MAC1105
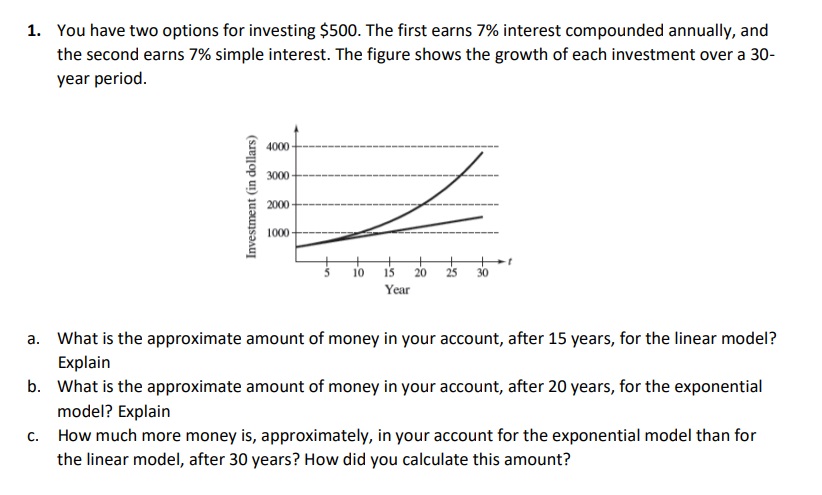
1. You have two options for investing $500. The first earns 7% interest compounded annually, and
the second earns 7% simple interest. The figure shows the growth of each investment over a 30-
year period
a. What is the approximate amount of money in your account, after 15 years, for the linear model?
Explain
b. What is the approximate amount of money in your account, after 20 years, for the exponential
model? Explain
c. How much more money is, approximately, in your account for the exponential model than for
the linear model, after 30 years? How did you calculate this amount?
Guide On Rating System
Vote
a. For the linear model with simple interest, the amount of money in your account after 15 years can be calculated using the formula A = P + rt, where A is the final amount, P is the principal amount ($500), r is the annual interest rate (7%), and t is the time in years (15).
Plugging in the values, we get A = $500 + 0.07 * $500 * 15 = $500 + $525 = $1025.
Therefore, after 15 years, you would have approximately $1025 in your account for the linear model with simple interest.
b. For the exponential model with compound interest, the amount of money in your account after 20 years can be calculated using the formula A = P(1 + r/n)^(nt), where A is the final amount, P is the principal amount ($500), r is the annual interest rate (7%), n is the number of compounding periods per year (1 for annually), and t is the time in years (20).
Plugging in the values, we get A = $500(1 + 0.07/1)^(1*20) = $500(1.07)^20 ≈ $1938.42.
Therefore, after 20 years, you would have approximately $1938.42 in your account for the exponential model with compound interest.
c. The difference in the amount of money in your account after 30 years between the exponential and linear models can be calculated by finding the difference between the final amounts for each model.
For the linear model after 30 years, the amount would be A = $500 + 0.07 * $500 * 30 = $500 + $1050 = $1550.
For the exponential model after 30 years, the amount would be A = $500(1.07)^30 ≈ $2564.38.
The approximate difference in the amounts would be $2564.38 - $1550 ≈ $1014.38.
Therefore, after 30 years, there would be approximately $1014.38 more money in your account for the exponential model than for the linear model.